机器之心报道

编辑：杜伟、+0

这几天，一篇关于向量嵌入（Vector Embeddings）局限性的论文在 AlphaXiv 上爆火，热度飙升到了近 9000。

要理解这篇论文的重要性，我们先简单回顾一下什么是向量嵌入。

向量嵌入就像把文字、图片或声音这些复杂的东西，转化成一个多维空间里的「坐标点」。比如，把「苹果」这个词变成一串几百维的数字，这些数字捕捉了它的语义（它可以指水果，也可以指公司）。在这个空间里，相似的概念彼此靠近，不相似的则远离。借助这种机制，计算机能够快速搜索或比较海量数据，而无需逐字逐句地比对。

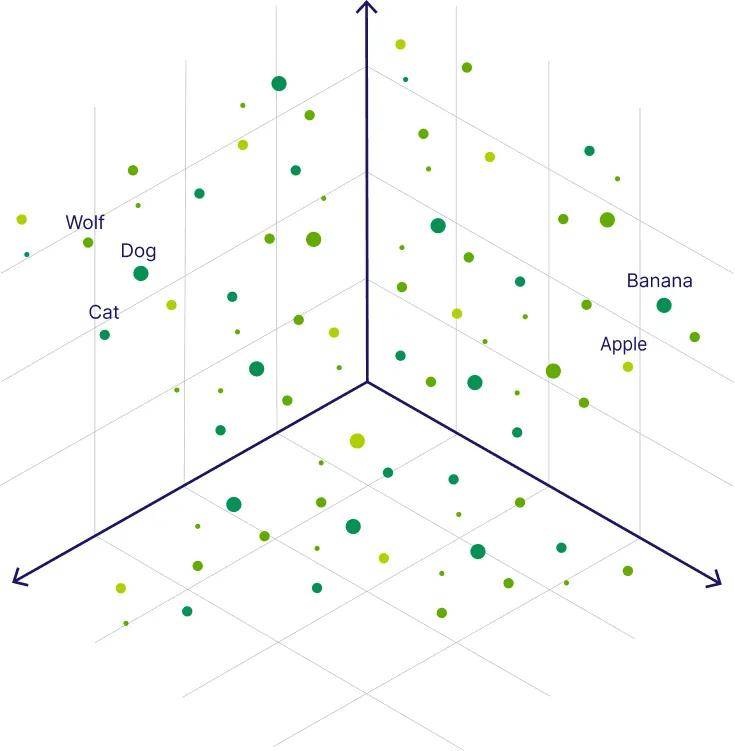
图源：veaviate

多年以来，嵌入主要用于「检索」任务，例如搜索引擎中的相似文档查找，或推荐系统中的个性化推荐。随着大模型技术的发展，嵌入的应用开始拓展到推理、指令遵循、编程等更复杂的任务。这些新兴需求，推动着嵌入技术朝着能处理任何查询、任何相关性定义的方向演进。

然而，先前的研究已经指出了向量嵌入的理论局限性。它的本质，是把一个高维度、复杂的概念（比如「爱」，可能包含亲情、爱情、友情、奉献、占有等无数面向）强行压缩成一串固定长度的向量。这个过程不可避免地丢失信息，就像三维苹果被拍成二维照片 —— 无论照片多清晰，你都无法从中还原出它的重量、气味等属性。

过去几年，业界普遍认为这种理论困难可以通过更好的训练数据和更大的模型来克服。这就是过去几年以 OpenAI 为代表的公司所遵循的「大力出奇迹」（Scaling Laws）的哲学。

从 GPT-2 到 GPT-4，再到 GPT-5，模型参数量和数据量指数级增长，能力也确实发生了质的飞跃。这让很多人相信，这条路能一直走下去。

然而，当前 AI 圈的一个热点争论就是：我们是不是快要撞上「Scaling Laws」的天花板了？

DeepMind 的最新研究为这个争论提供了新的证据。他们将几何代数与通信复杂度理论结合，证明了向量嵌入的能力存在一个数学下界：对于任意给定的嵌入维度 d，当文档数量超过某个临界点时，总会存在一些相关文档组合是无论如何都无法通过查询同时召回的。

这意味着，嵌入模型存在一个不可逾越的限制，无法单纯依靠「更大的模型」来突破。

• 论文标题：On the Theoretical Limitations of Embedding-Based Retrieval
• arXiv 地址：https://arxiv.org/pdf/2508.21038

这一理论瓶颈在现实中最直接的体现，就是检索增强生成（RAG）。RAG 的工作机制是：先用向量嵌入从知识库中检索相关信息，再交给大模型生成答案。但 DeepMind 的证明表明，当知识库规模足够大、一个问题需要多份文档共同回答时，即使采用最先进的嵌入模型，也可能因为维度不足而无法完整召回关键信息。这会导致大模型在生成时受到错误或不完整上下文的干扰。

为了证明这一理论限制对任何模型或训练数据都成立，研究者采用了一种「最佳情况」设定，即向量本身是使用测试数据直接进行优化的。实验发现，对于每个嵌入维度 d 都存在一个临界点，一旦文档数量超过该点，嵌入维度就不足以编码所有的组合。他们还证明了这种临界关系可以通过一个多项式函数进行经验性建模。

更进一步，研究者基于这些理论局限性构建了一个名为 LIMIT 的简单数据集。尽管任务很简单（例如，「谁喜欢苹果？」），但即便是 MTEB 基准上最先进的嵌入模型也很难解决这个问题，而对于嵌入维度较小的模型来说则是不可能的。

论文一作、约翰霍普金斯大学博士生 Orion Weller 表示，在当前的信息检索领域，大家希望嵌入模型能够同时承担指令理解和推理等一切能力。遗憾的是，单向量嵌入模型在理论和实证上都做不到，它们存在根本性限制。通过开源的简单评测任务，他们证实了即便是 SOTA 模型也表现糟糕。

总的来说，这篇工作的贡献可以总结为以下三点：

• 为嵌入模型的根本性局限提供了理论基础；
• 通过自由的嵌入优化进行最佳情况下的经验性分析，证明了该理论适用于任何数据集实例；
• 构建了一个名为 LIMIT 的简单、真实的自然语言实例，即使是最先进的嵌入模型也无法解决。

这不仅揭示了 RAG 系统在应用上的硬性约束，也让人重新思考 Scaling Laws 在 AI 发展中的边界。嵌入的局限，也许正是「加大规模」并非万能解法的一个缩影。

向量嵌入的表征能力

研究者首先证明了通信复杂性理论中的已知结果在向量嵌入设定下的含义。

理论上限。对于二进制矩阵，逐行排序和逐行阈值化是等价的表征能力概念。

到目前为止，研究者描述的这些概念与矩阵的符号秩密切相关。在本文的其余部分，他们将利用符号秩来建立主要的界限。

将所有这些结合起来就得出了所需的不等式链。

研究者表示，在向量嵌入模型的背景下，这为准确捕获一组检索目标所需向量的维度提供了上下界，无论是逐行排序、逐行阈值，还是全局阈值。

具体来说，给定某个二进制相关矩阵 A ∈ {0,1}^m×n，至少需要 rank_±(2A − 1_m×n) − 1 个维度来精确捕获 A 中的关系，并且最多需要 rank_±(2A − 1_m×n) 个维度就能实现。

在实际中，这意味着：

• 对于任意固定的维度 d，都会存在某个二进制相关矩阵无法通过 d 维嵌入来捕获，这是因为存在符号秩任意高的矩阵。换句话说，那些 qrel 矩阵具有更高符号秩的检索任务更难被嵌入模型精确捕获，需要更高的嵌入维度。
• 如果能够在 d 维中以逐行保持顺序的方式嵌入某个给定的矩阵 A ∈ {0,1}^m×n，那么这就意味着 2A − 1_m×n 的符号秩有一个上界。这尤其表明了一种实用机制，可以通过对自由嵌入表示进行梯度下降优化来确定矩阵符号秩的上界。

实证联系

最佳情况优化

在上文中，研究者已经基于 qrel 矩阵的符号秩及其嵌入维度 d 建立了嵌入模型的理论局限，现在希望在实证层面上也展示这一点。

为了展示可能的最强优化情况，研究者设计了实验，使得向量本身可以通过梯度下降直接优化。他们称这种方式为「自由嵌入」优化，嵌入是自由可优化的，不受自然语言的限制，而自然语言会对任何现实的嵌入模型施加约束。因此，这可以展示任意嵌入模型是否有可能解决该问题：如果自由嵌入优化无法解决该问题，那么真实的检索模型也无法做到。

值得注意的是，研究者是通过直接在目标 qrel 矩阵（测试集）上优化嵌入来实现的。这种方式不会泛化到新的数据集，但其目的是展示可能出现的最高性能。

关于实验设置，研究者创建一个随机文档矩阵（大小为 n）和一个随机查询矩阵，其中包含 top-k 集合（所有组合，即大小为），两者均为单位向量。然后直接使用 Adam 优化器来优化约束条件。每一次梯度更新都对所有正确的三元组进行完整遍历（即整个数据集作为 batch-size），并使用 InfoNCE 损失函数，其他所有文档作为批内负样本（即整个数据集在一个 batch 中）。

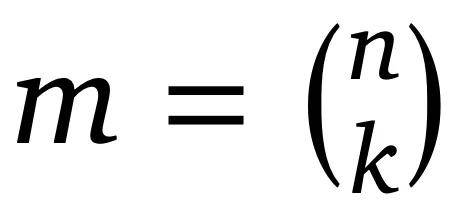
由于几乎所有嵌入模型都使用归一化向量，研究者也同样采用这种方式（在更新后进行归一化）。当损失在 1000 次迭代中没有改进时，就提前停止。他们逐渐增加文档数量（因此查询的组合数也随之增加），直到优化器无法再解决该问题（即无法达到 100% 的准确率）。研究者将这一点称为「临界 n 点」。

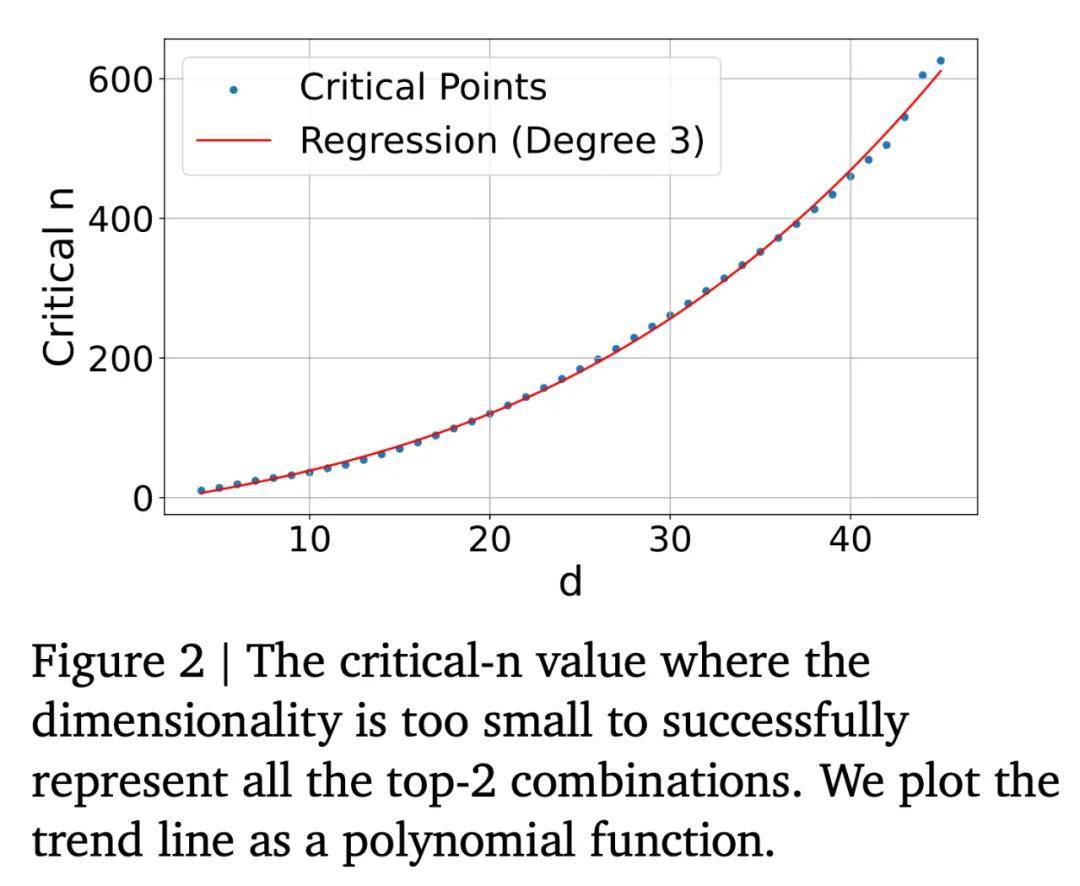
由于文档数较大时组合数量呈现组合爆炸（例如 5 万个文档、top-k=100 时会产生 7.7e+311 种组合，这相当于自由嵌入实验中维度为 d 的查询向量数量），因此研究者专注于 n、k 和 d 的相对较小规模。研究者设定 k=2，并在每个 d 值下逐次增加 n，直到模型无法解决问题。此外对数据拟合了一条多项式回归曲线，以便能够建模并向外推算结果。

结果如下图 2 所示，该曲线符合三次多项式拟合，其公式为 y = −10.5322 + 4.0309d + 0.0520d² + 0.0037d³ （r²=0.999）。将该曲线外推得到的临界 n 值（对应嵌入维度）分别为：500k（512）、170 万（768）、400 万（1024）、1.07 亿（3072）、2.5 亿（4096）。

需要注意，这只是最佳情况：真实的嵌入模型无法直接优化查询和文档向量以匹配测试集的 qrel 矩阵，并且还受到「自然语言建模」等因素的约束。然而，这些数值已经表明，对于网页级别的搜索，即便是在理想测试集优化下，最大的嵌入维度也不足以建模所有组合。

实证联系

真实世界数据集

接下来，研究者将（1）该理论与现有数据集建立联系；（2）为现有 SOTA 模型构建一个极其简单却又极度困难的检索任务。

与以往工作形成对比的是，研究者希望构建的数据集，可以用于评估少量文档情况下所有 top-k 集合的组合。不同于使用 QUEST、BrowseComp 等复杂的查询操作符（这些操作本身就因 qrel 矩阵之外的原因而很难），他们选择了非常简单的查询和文档，以突出表示所有 top-k 集合本身的难度。

LIMIT 数据集

研究者选用 5 万个文档，以构建一个既有难度又相对规模较小的语料库；同时使用 1000 个查询，以在保证统计显著性的前提下仍能快速完成评估。

对于每个查询，研究者选择关联两个相关文档（即 k=2），这样做既为了简化实例化过程，也为了与之前的工作保持一致。接下来是选择一个 qrel 矩阵来实例化这些属性，并为查询分配随机的自然语言属性，将这些属性添加到各自的相关文档中（参见图 1）。

研究者测试了所有文档组合的相关性（对于三个文档，每个查询包含两个相关文档的所有组合），并通过一个简单的映射进行实例化。

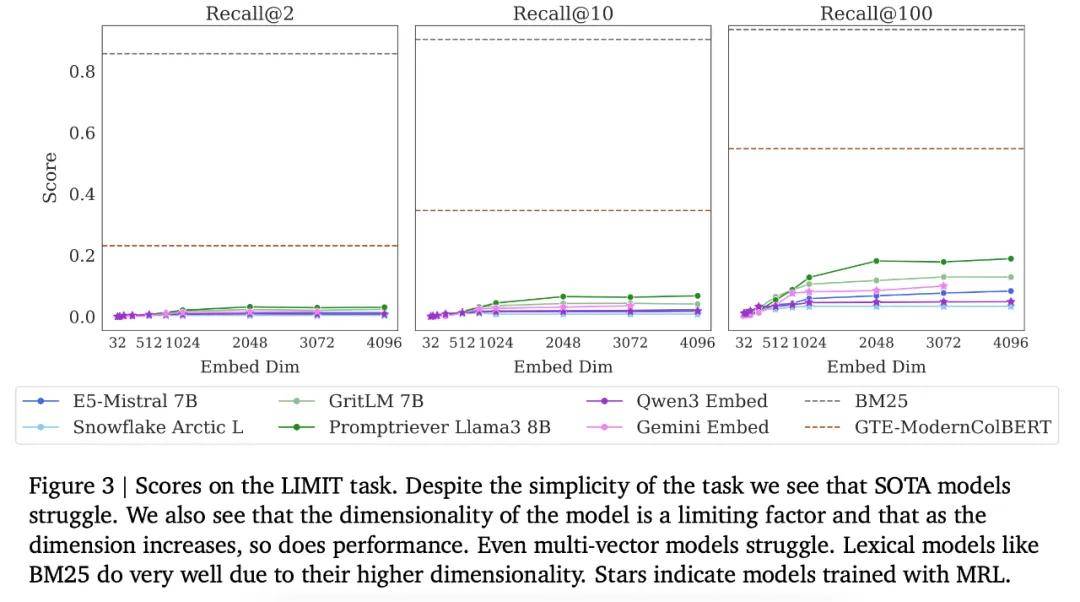
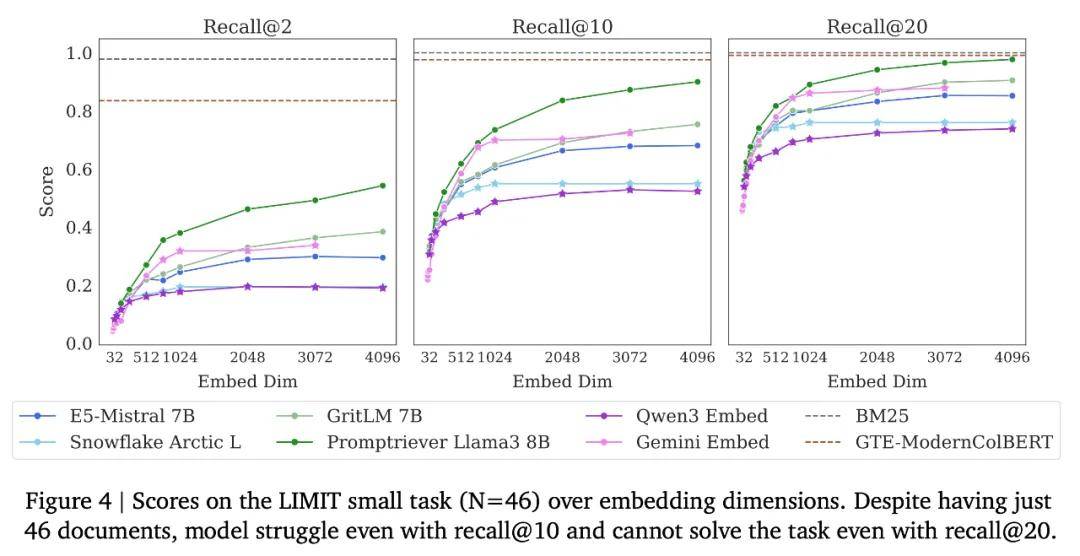
研究者评估了当前 SOTA 嵌入模型，包括 GritLM、Qwen 3 Embeddings、Promptriever、Gemini Embeddings、Snowflake 的 Arctic Embed Large v2.0 以及 E5-Mistral Instruct，并展示了在完整嵌入维度下的结果以及在截断嵌入维度（通常用于 matryoshka learning，即 MRL）下的结果。

下图 3 展示了在完整 LIMIT 上的结果，而下图 4 展示了在小规模（包含 46 个文档）版本上的结果。令人惊讶的是，即便任务本身很简单，模型依然表现极差。在完整设置中，模型甚至难以达到 20% 的 recall@100，而在 46 个文档的版本中，即使是 recall@20，模型也无法解决该任务。

存在领域迁移吗？

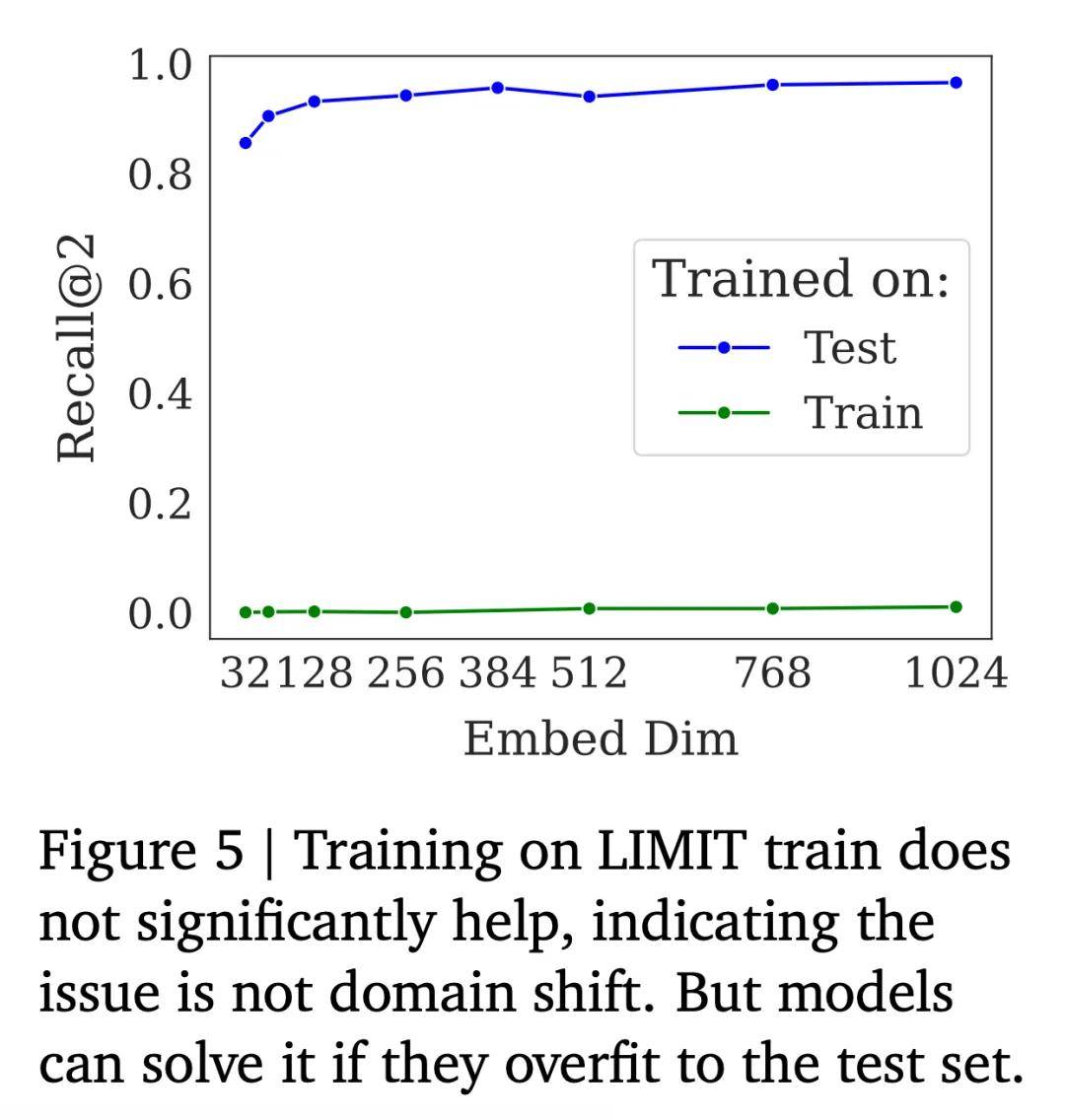
虽然本文的查询看起来与标准的网页搜索查询相似，但研究者怀疑是否存在某种领域迁移从而导致性能低下。如果真是这样，那么在相似示例的训练集上进行训练预计能够显著提升性能。另一方面，如果任务本身就很难，那么在训练集上训练几乎无济于事，而在测试集上训练则会让模型过拟合到特定 token。

下图 5 显示，在训练集上训练的模型无法解决该问题，虽然 recall@10 从最开始的接近零有了轻微提升，最高达到了 2.8。但在域内训练时并未出现明显的性能提升，表明性能较弱并不是由领域迁移造成的。

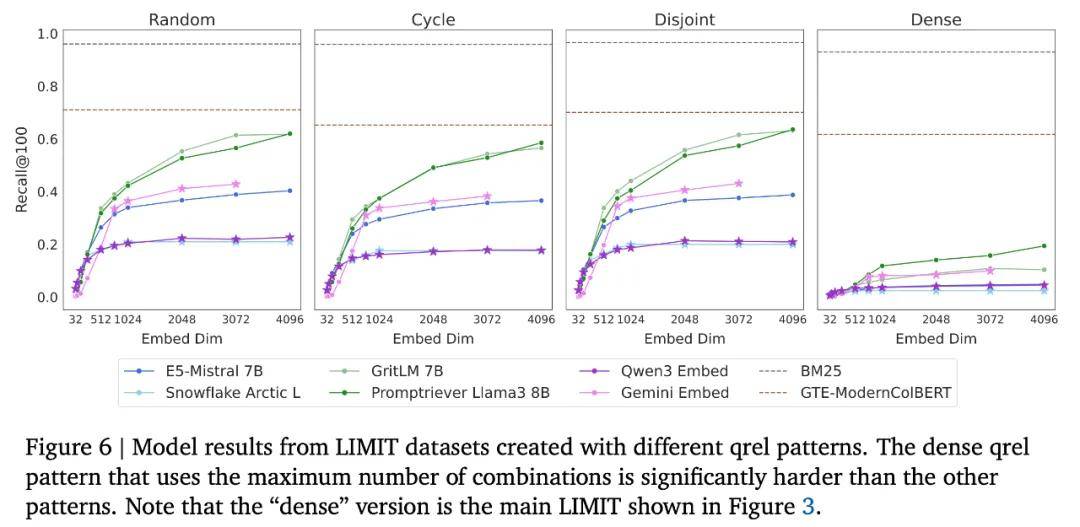
Qrel 模式的影响

研究者从以下四种不同的 qrel 模式来实例化 LIMIT 数据集：

• 从所有组合中随机采样；
• 基于循环的设置，其中下一个查询与前一个查询中的一个文档以及后续下一个文档相关；
• 不相交模式，每个查询与两个新的文档相关；
• 在查询集中能容纳的最大文档数上，最大化连接数（即组合数 n choose k）的模式（稠密模式，标准设置）。

从下图 6 可以看到，除了稠密模式之外，其他模式的性能相对接近。不过，当转向稠密模式时，所有模型的分数都显著下降：GritLM 的 recall@100 绝对值下降了 50，而 E5-Mistral 的降幅更加惊人，几乎降低了 10 倍（从 40.4 降到了 4.8）。

更多技术细节和实验结果请参考原论文。