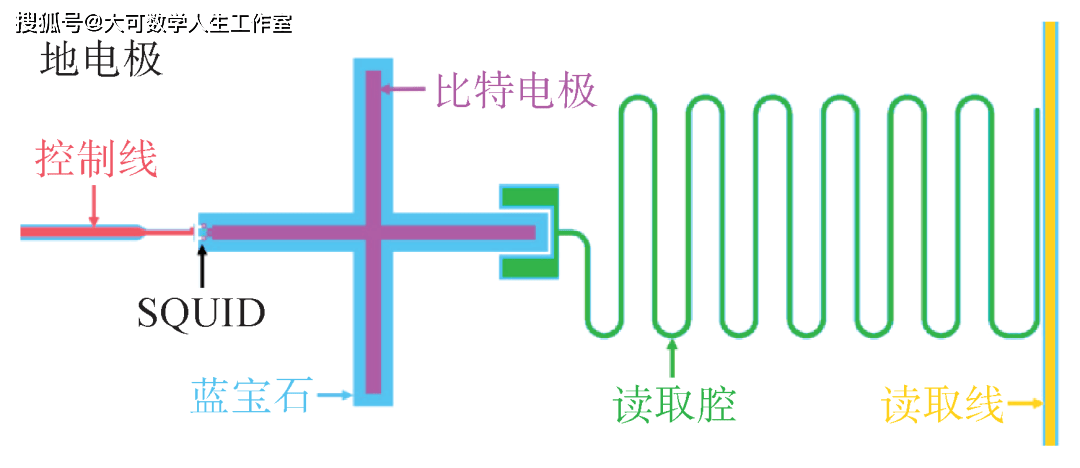
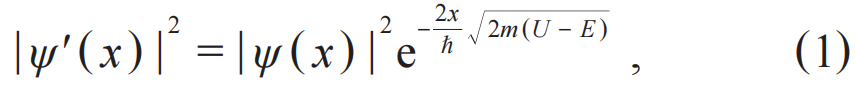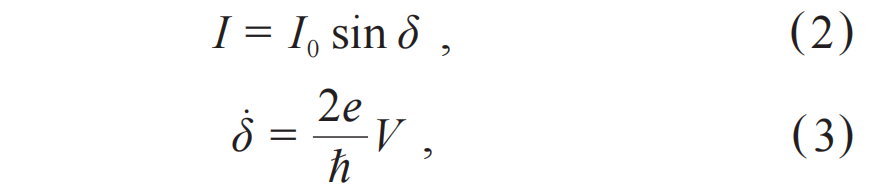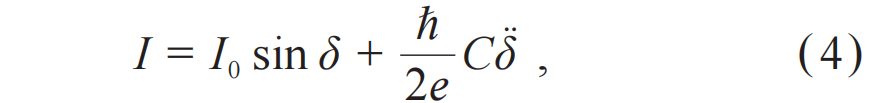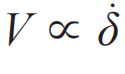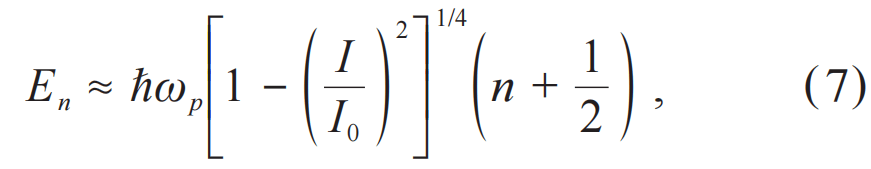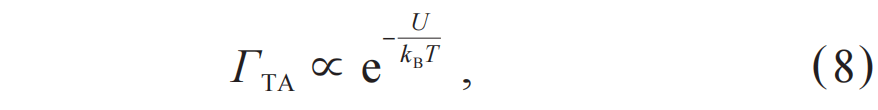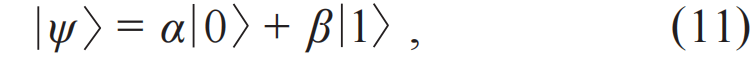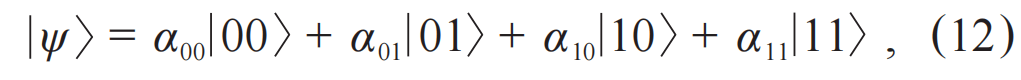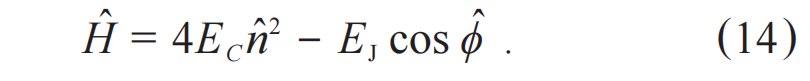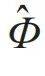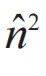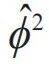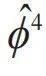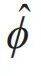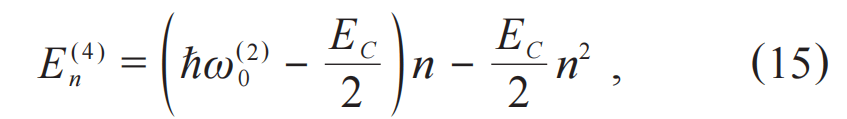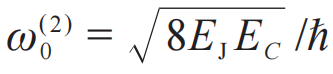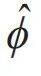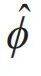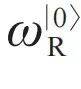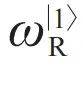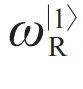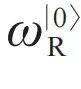宏观量子效应与超导量子计算—
|作者:梁珪涵 时运豪 许凯 范桁†
(中国科学院物理研究所)
本文选自《物理》2025年第11期
摘要 2025年诺贝尔物理学奖表彰了电路中宏观量子效应的实验验证,这项发现为当前蓬勃发展的超导量子计算技术奠定了物理基础,文章旨在介绍其原理与影响。首先详细介绍获奖内容,从量子隧穿与宏观量子隧穿的基本原理讲起,阐述超导体与约瑟夫森结如何为观测这些效应提供理想平台,之后介绍获奖者们如何通过精密的实验手段验证这些宏观量子现象。最后,将进一步探讨基于这些宏观量子效应发展起来的超导量子计算技术,内容涵盖其基本原理、实现方法以及当前的发展现状与未来展望。
关键词 宏观量子隧穿,能量量子化,超导电路,约瑟夫森结,超导量子计算
01
诺奖内容介绍
瑞典皇家科学院将2025年诺贝尔物理学奖授予美国加州大学伯克利分校的约翰·克拉克(John Clarke)、耶鲁大学的米歇尔·德沃雷特(Michel H.Devoret)和加州大学圣芭芭拉分校的约翰·马蒂尼斯(John M. Martinis)(图1),表彰其“电路中宏观量子隧穿和能量量子化的发现”(For the discovery of macroscopic quantum mechanical tunnelling and energy quantization in an electric circuit)。

图1 2025年诺贝尔物理学奖得主:克拉克、德沃雷特、马蒂尼斯(图片来源于诺贝尔奖官网)
三位获奖人的获奖成果是发表于1985年的两篇Phys. Rev. Lett.文章,6月份投稿的Phys. Rev. Lett.55,1543(1985)[1]和7月份投稿的Phys. Rev. Lett. 55,1908(1985)[2],分别基于约瑟夫森结系统确认了超导电路中的能量量子化和宏观量子隧穿。这两篇主要的工作只有这三位获奖人署名,当时克拉克是教授,德沃雷特是博士后,而马蒂尼斯是高年级博士生。
在这一章中,我们首先介绍量子隧穿与宏观量子隧穿究竟是什么,之后再阐述为什么超导体和约瑟夫森结是诺奖工作的实验基础,最后就可以一起了解三位获奖人是如何从实验中真正观察到这些现象了。
1.1 量子隧穿与宏观量子隧穿
量子隧穿效应(quantum tunneling effect)作为量子世界的标志性现象之一,其宏观扩展——宏观量子隧穿,是诺奖工作的核心[3,4]。量子隧穿是指一个微观粒子能够穿过一个在经典物理学看来其能量无法逾越的势垒的现象。我们可以用一个简单的比喻来说明,如图2所示:在经典物理学的情况下,若是想将一个小球扔过一堵高墙,我们必须将其扔得足够高,超过墙的高度,小球才能越过高墙到达另一边,否则就像左图所示的一样被墙壁弹回来;在量子的世界中,这堵高墙就是上面所说的势垒,小球就是微观粒子,而墙壁的高度和小球被扔起的高度就代表它们各自能量,但此时就算小球被扔出的高度低于墙壁的高度,小球依然有一定的概率穿过墙壁出现在另一边,如右图所示,仿佛就像墙壁上被打开了一个隧道一样让小球通过,这就是量子隧穿。

图2 左图表示经典世界中小球碰到墙壁会被弹回来,右图表示量子世界中粒子遇到势垒会有一定概率隧穿过去
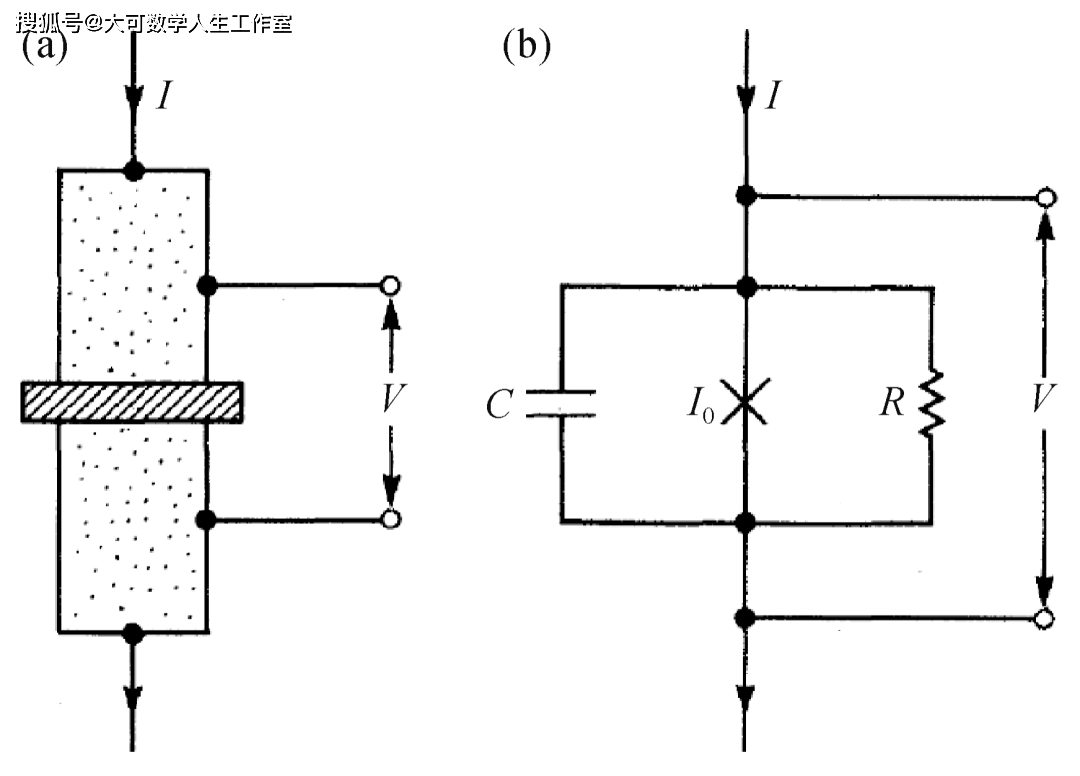
量子隧穿源于微观粒子的波动性。在量子力学中,微观粒子的状态由一个波函数ψ(x)描述,其中x代表其位置。波函数本身没有物理意义,但其模方|ψ(x)|2代表了在位置x处找到该粒子的概率。假设势垒的宽度为L、高度为U,粒子的质量为m、能量为E 其中,ℏ=h/2π是约化普朗克常量,h≈6.626×10-34 J·s是普朗克常量,并且在穿过势垒后,粒子的波函数始终保持为ψ'(L)。因此,只要势垒的宽度是有限的,波函数在穿过势垒后就可以不为零,意味着粒子会出现在势垒的另一边,即发生了隧穿。其中需要注意的是,对于单个粒子而言隧穿过程是随机的,我们无法预测某一个粒子是否会隧穿,只能给出它隧穿的概率|ψ'(x)|2/|ψ(x)|2。假设电子穿过宽度为2 nm的势垒,并且与势垒的能量差为1 eV,那么其隧穿的概率大约为1.3×10-9。这一概率看似很小,但实际上电子每秒钟撞击势垒的次数超过109量级,因此每秒钟依然可以有大量电子隧穿过这一势垒,这就形成了量子隧穿。 事实上,量子力学认为所有的物体都具有波粒二象性[5],我们也可以从这一角度来看隧穿是否可以发生。物体的波动性由德布罗意波波长λ=h/p决定,p=mv是物体的动量。当德布罗意波波长大于或接近物体的尺寸时,物体就会体现出波动性,从而更具备量子的特性;而若是德布罗意波波长远小于物体的尺寸时,物体几乎不具备量子的特性,从而可以认为它是经典的。对于宏观物体,其德布罗意波长极短,隧穿概率小到在物理上可以忽略不计。 宏观量子隧穿(macroscopic quantum tunneling,MQT)指的并不是一个宏观物体能够产生隧穿效应,例如一颗球或一个人。它指的是一个系统的某种宏观变量作为一个整体能够表现出量子隧穿的行为,例如电路中的电流、磁通量或电压。具体而言,假设在微米级尺度的电路中插入纳米级的绝缘体,如果我们只单纯从波粒二象性的角度看,微米级尺度电路的德布罗意波长远小于纳米级,这一模型就会被看成经典的,是一个电流无法通过绝缘部分的开路电路情况。宏观量子隧穿效应使电流作为宏观变量整体发生量子隧穿,从而维持电路导通。这种隧穿并非单个粒子的随机行为,而是所有粒子的集体效应。 不过,想要实现宏观量子隧穿需要非常苛刻的条件,需要让大量粒子组成的宏观系统以一种完美协同的方式运动,即所有粒子保持相干。单个粒子的波函数可以被简化写为ψ=Aeiϕ,其中A是振幅,决定了波的强度,而ϕ是相位,决定了波在其周期中所处的位置。所有粒子保持相干其实就是要求它们的相位是统一变化的,从而可以让所有粒子的集合被看成一整个更大的波函数,成为一个宏观变量,实现宏观相干系统。 因此,实现宏观量子隧穿需满足以下条件:其一,系统需具备宏观相干性,即存在可被量子化的宏观变量;其二,需接近绝对零度的极低温环境以抑制热噪声,从而削弱破坏相干性的随机热振动;其三,系统需与外界高度隔离且自身损耗极低,以确保构成宏观变量的微观粒子保持相干,避免外界干扰或系统损耗引发集体退相干。三位获奖人发现,超导体中的库珀对正是满足上述条件的准粒子,而含约瑟夫森结的超导电路则是实现宏观量子隧穿的理想系统。 1.2 超导体和约瑟夫森结 超导体是某一类特定的材料,当它被冷却到某个临界温度Tc以下时会进入超导态,从而表现出零电阻和迈斯纳效应两个特性。零电阻即电流可以在超导体中完全无耗地流动,使其成为真正的理想导体;迈斯纳效应让超导态下的超导体将其内部的所有磁场主动排出,使其成为完美的抗磁体。 BCS理论为我们揭示了超导体的微观机理[6],当超导体的温度低于临界温度时,超导体中的电子移动会吸引周围的正离子,从而产生称为声子的晶格振动。通过这种声子作为媒介,每两个电子可以克服它们之间的排斥力,形成一个被称为库珀对(Cooper pair)的整体。这一过程将作为费米子(Fermion)的电子转变为了作为玻色子(Bosons)的库珀对,而玻色子在极低温下会发生玻色—爱因斯坦凝聚(Bose—Einstein condensation,BEC)[7,8],导致所有库珀对全部凝聚到同一个能量最低的基态,形成一个相干的整体。 因此,超导体天然就是一个宏观量子相干的系统,同时其零电阻的特性也满足系统本身有极低损耗的条件,我们只需要让系统保持在极低温的环境中,让超导体保持在超导态,并控制好外部环境的干扰,就能让超导系统成为可以实现宏观量子隧穿的平台。 图3 (a)约瑟夫森结的结构示意图,带点的部分为超导体,两个超导体之间带斜杠的部分为绝缘体;(b)约瑟夫森结电路模型,×代表约瑟夫森结[10] 接着,就需要在超导系统中引入一个势垒,约瑟夫森结是一个最佳选择,电流偏置的约瑟夫森结如图3所示[9,10]。图3(a)展示了约瑟夫森结由超导体—绝缘体—超导体组成,施加的偏置电流I可以穿过结区,测量结两端的电压差V。图3(b)展示了其电路模型,由电容C、约瑟夫森结I0和电阻R组成,其中电阻用于代表系统中的所有耗散,通常与频率有关。 理想约瑟夫森结的两个约瑟夫森关系为: 其中I0代表约瑟夫森结的临界电流,若穿过结的电流超过I0,会使结变为一个普通电阻,不再满足约瑟夫森关系。公式(2)是直流方程,将穿过结的电流I与宏观相位δ联系起来;公式(3)是交流方程,根据结两端的电压V给出了δ的时间演化。 如果忽略耗散,即忽略电阻R,考虑上交流电压通过电容的电流,可以将图3所示的约瑟夫森结电流表示为: 可以将公式(4)解释为一个以δ为坐标变量的虚构粒子的牛顿方程,其质量与电容成正比。作用在该粒子上的力是保守力,将其对坐标积分可以得到倾斜“搓衣板”势: 其中EJ=ℏI0/2e,被称为约瑟夫森能。可以控制偏置电流I:如果其低于临界电流,即I 图4 倾斜搓衣板势 (a)在I 另外,我们还可以将这个倾斜搓衣板势在局部最小值的底部进行展开,从而将其近似为一个谐振子势能: 其中δ0代表势能取局部最小值的相位。由这个近似的谐振子势能,便可以求出其分立能级: 其中,被称为约瑟夫森等离子体频率,代表在I=0搓衣板势未倾斜时,粒子在局部最小值底部的振荡频率。不过这里的能级计算用了谐振子近似,所以得到了等间隔分布的线性能级,实际上约瑟夫森结的能级应该是非线性的,这一点我们会在2.1小节中进一步介绍。再次说明,上述的粒子其实指的是超导体中的库珀对集体,其相位δ是一个宏观变量,因此意味着超导电路中的是宏观量子隧穿和能量量子化。 1.3 宏观量子隧穿和能量量子化的实验验证 实验上,可基于图3所示的约瑟夫森结,在不同温度下逐步增大偏置电流,并同步监测结两端电压的变化。通过重复该测试过程,可观测到宏观量子隧穿现象的发生。在不同温度下开展实验的关键意义在于,能够有效区分粒子逃逸的经典热激活机制与量子隧穿机制。在较高温度下,粒子可通过经典方式获取热能kBT,从而越过势垒实现逃逸。根据克拉默斯逃逸速率理论[11],此时逃逸速率与温度呈正相关关系: 其中kB是玻尔兹曼常数,U是势垒高度。在温度降低到一定程度时,比如低于100 mK,热激活导致的逃逸速率会非常小,而此时与温度无关的量子隧穿导致的逃逸速率ΓMQT就会占据主导。ΓMQT的形式和公式(1)类似,与势垒高度、粒子的等效质量等相关。实际上,总的逃逸速率始终等于热激活导致的速率与隧穿导致的速率之和,即Γ=ΓTA+ΓMQT。可以定义一个有效逃逸温度Tesc来表示它: 因此,若发现随着温度降低,测到的有效逃逸温度从与实际温度相关逐渐变为无关,这个转变点的温度也被称为交叉温度,这一现象意味着宏观量子隧穿的存在。 其次,需要逐渐增加偏置电流来提高粒子逃逸的几率。粒子逃逸是一个泊松过程,在恒定的逃逸速率Γ 下,经过任意时间t 后,粒子累积的逃逸概率为: 其与势垒高度是负相关的。当偏置电流I很小时,搓衣板势比较平,势垒会很高,粒子逃逸速率极低,需要等待极其漫长的时间才可能观测到逃逸;当逐渐增加偏置电流,让搓衣板势逐渐倾斜,从而使势垒变得更低,增加了粒子的逃逸速率,在短时间内就能观测到逃逸。实际测试中,这个逐渐增加偏置电流的速率vI=dI/dt是关键,需要足够缓慢,比如vI=1 μA/s甚至更低的速率。这样缓慢的增加速率相当于在每个微小的偏置电流窗口ΔI内,都进行了时间为Δt=ΔI/vI的观测。当偏置电流缓慢增加时,逃逸速率随之增加,当它增加到足够大,使得此时的逃逸概率P(Δt)变得不可忽略时,可以观察到这个随机的粒子逃逸,此时的电流称为逃逸电流Iesc。 接着,监测结两端的电压来观测逃逸的发生。当粒子没有发生逃逸时,粒子被困在势阱中,根据公式(3)可知,相当于相位没有变化,=0,因此结两端的电压为零;当逃逸发生时,粒子开始在搓衣板势上运动,其相位开始变化,≠0,从而产生非零的电压。因此在逐渐增加偏置电流的过程中,发现结两端的电压从零跳变为非零的瞬间,就是粒子逃逸发生的瞬间,此时记录下的电流就是逃逸电流。 最后,不断重复进行逃逸电流的测试,从中提取出总逃逸速率和有效逃逸温度。由于逃逸是随机事件,因此重复测出的逃逸电流并不会是一个固定值,而是有一个分布。一般我们会重复上万次测量,获得逃逸电流的概率密度函数p(Iesc)。最后,根据系统从亚稳态逃逸的概率分布[12],拟合出在逃逸电流平均值处Iesc的总逃逸速率Γ(Iesc),再根据公式(9)就可以得到有效逃逸温度。 但需要尤其注意的是,在降温时这种逃逸速率变得与温度无关的现象也可以用过量噪声(excess noise)来解释,即系统本身与用于测量温度的温度计不在热平衡状态,例如实验中的某些装置较热的部分发出的微波黑体辐射。因此,在搭建这样一套测试系统时,必须消除这种过量噪声,让实验结果与理论有很好的对应,才能真正证明这是宏观量子隧穿导致的逃逸。 三位获奖人的原始工作是在美国加州大学伯克利分校完成的。他们在稀释制冷机中精心设计了滤波器链路,在0.1 GHz到12 GHz的频率范围内提供了超过200 dB的衰减。考虑到滤波器本身的黑体辐射是在其自身温度下发出的,因此在制冷机的不同温度区域中将滤波器链路进行热锚定(thermal anchoring)是非常重要的。利用这一套装置,他们排除了过量噪声的影响,成功测出了有效逃逸温度在高温时与实际温度相关,而在温度降低时逐渐与实际温度无关的现象,证明了宏观量子隧穿的发生。 图5 有效逃逸温度关于实际温度的测量数据,横坐标上标记的白色箭头代表经典结的交叉温度,黑色箭头代表量子结的交叉温度[2] 如图5所示,实验上测试了两种约瑟夫森结的有效逃逸温度,一种被称为量子结(quantum junction),另一种被称为经典结(classical junction)。量子结就是我们上述的约瑟夫森结,其临界电流较高;而经典结则是通过施加特定的磁场抑制了临界电流I0,使其临界电流更低,从而使搓衣板势的势垒高度低于量子结。因此,根据公式(8),更低的势垒高度意味着,在与量子结处于相同的温度下,经典结的热激活导致的逃逸速率更大,从而测出了比量子结更低的交叉温度。经典结和量子结互相对照,证明了实验结果与理论对应的可靠性,说明交叉温度的产生并不是由噪声或其他干扰造成的,让它成为了证明宏观量子隧穿存在的确凿证据。 该实验装置的另一关键组成部分是一条可实现约瑟夫森结共振激活(resonant activation)的弱耦合微波控制线[13]。在没有共振激活的情况下,实验可以测出结的临界电流I0。共振激活时可以测出结的等离子体频率,即公式(7)中的ωp,从而确定图3中的电容C。共振激活的宽度可以用来表征阻尼电阻,即图3中的电阻R。因此,理论中的所有输入参数都可以通过实验独立确定,极大增强了数据拟合的可靠性。 图6 (a)对约瑟夫森结施加2 GHz的微波时,逃逸功率相对于不施加微波时的变化;(b)约瑟夫森结在不同近邻能级间跃迁频率的理论计算曲线[1] 除此之外,共振激活还允许对结的宏观状态进行微波光谱分析,从而可以得到宏观能量量子化的直接证据,如图6所示。图6(a)是在对约瑟夫森结施加2 GHz微波时测量的逃逸速率,Γ(0)代表没有施加微波时的逃逸速率,Γ(P)代表施加微波时的逃逸速率,因此纵坐标代表了施加微波后,逃逸功率相对增加了多少。横坐标是施加在约瑟夫森结上的偏置电流I,根据公式(7),电流改变时,约瑟夫森结的分立能级En也会改变。实验数据表明,在施加了2 GHz的微波时,在几个特定的偏置电流下,逃逸速率会显著增加。 图6(b)的纵坐标代表的是几个不同近邻能级En之间的跃迁频率,横坐标依然是偏置电流I。从左到右三条倾斜的实线分别是从n=2到n=3、n=1到n=2和n=0到n=1的跃迁频率的理论计算曲线,它们与微波频率En,n+1/h=2 GHz的三个交点与图6(a)中三个逃逸速率显著增加的点正是处于相同的横坐标位置,如各自图中的三个箭头所示,即相同的偏置电流。这是因为当跃迁频率等于微波频率时,粒子就能最有效地吸收微波能量,从而跃迁到更高的能级,更接近势垒顶部,如图6(a)右上角的插图所示,因此提高了跃迁速率。这一实验结果非常有力地证明了在超导电路中,即宏观量子系统中的能量量子化。 综上所述,研究团队利用超导电路这一实验平台,不仅观测到宏观库珀对集体行为所表现出的量子隧穿现象,更通过精确测量其分立的量子化能级,使二者互为印证,为宏观尺度下的量子隧穿与能量量子化提供了确凿的实验证据。这一成果标志着量子力学规律在由亿万粒子组成的宏观系统中同样成立,获得了决定性的验证。 该项奠基性工作为后续新型超导器件的探索奠定了理论基础,其中超导二极管效应的提出与实现尤为引人注目。该效应的核心机制在于约瑟夫森结中引入的电子/空穴掺杂不对称结构,使得电流在正向传导时保持无耗散的超导态,而在反向传导时转变为有电阻的正常态[14—18]。从物理本质上看,这源于对诺奖所揭示的量子隧穿特性的深化应用——通过打破量子隧穿的对称性,实现了电流的单向无耗散传输,为低功耗超导电子学开辟了新路径。图3所示的约瑟夫森结结构,正是实现此类不对称势垒调控的理想平台。 除了推动超导电子学领域的突破,今年的诺奖工作也直接促进了超导量子计算的蓬勃发展,我们将在下一章展开详细论述。 02 超导量子计算 三位获奖人的工作是超导量子计算技术的基础,自1994年肖尔算法(Shor’s algorithm)[19]发明之后,科学家们开始了实现量子比特(即可控的量子二能级系统)的探索,诺奖工作发现的宏观量子效应使超导电路成为实现量子比特的平台之一。 1999年,东京大学及日本电气公司(NEC)物理学家中村泰信(Nakamura)和蔡兆申等基于本次诺奖工作的类似原理制备出了第一个超导量子比特[20],这一工作启发了许多用于量子信息处理的超导电路新设计[21]。后来,随着电路量子电动力学(circuit quantum electrodynamics,cQED)的进步,量子比特电路发展出了可以高保真非破坏性地读取比特状态的方法[22,23]。2007年,一种被称为Transmon的超导量子比特由于其对电荷噪声的不敏感性以及优秀的可扩展性[24],成为了实现大规模量子计算的有力方案。 接下来,我们基于Transmon对超导量子比特的原理、超导量子计算的实现,以及其发展现状与未来进行介绍。 2.1 超导量子比特的原理 对于量子比特而言,我们一般只用到比特的基态和第一激发态作为|0>态和|1>态,可以类比成经典计算中每个比特的状态0和1,不过与经典计算只能确定地处于0或者1不同,由于量子态的叠加性,量子比特可以处于|0>和|1>的线性叠加态: 其中α和β是复数,为概率幅,满足归一化条件|α|2+|β|2=1。 考虑两个量子比特的情况,其状态类似于经典比特的4种组合|00>、|01>、|10>和|11>,每组的两个数字分别代表每个比特的状态,其叠加态可以表示为: 其概率幅αx(x∈{0,1}2)依然满足归一化条件∑|αx|2=1。在两比特没有纠缠时,该状态可以被写为直积态的形式,即状态等于两个比特各自叠加态的直积,可以对其中一个比特进行测量而不影响另一个的比特状态。但当两比特处于纠缠态时,例如贝尔态: 纠缠态与直积态有很大的不同,它们之间具有很强的关联性,测量其中一个比特的状态后,另一个比特的状态也就确定了。 叠加态和纠缠态的存在使得量子计算机能够实现并行运算,即在n量子比特的系统下,理论上可以对2n个比特序列进行同时运算。因此,量子计算表现出了指数级增长的信息存储与处理能力,这是经典计算机无法比拟的,也是量子优势的核心来源。 图7 单个接地Transmon比特等效电路图 我们现在常用的单个接地Transmon比特被称为Xmon[25],其等效电路如图7所示,其中包含了紫色示意的比特本身的部分,红色示意的包含了激发和偏置的控制线部分,绿色示意的读取腔部分和黄色示意的读取线部分。控制线的激发部分可以将比特从|0>态激发到|1>态,偏置部分可以改变比特在|0>态和|1>态之间的跃迁频率。读取腔和读取线配合,可以共同实现对比特状态的非破坏性读取。 比特由一个接地的超导量子干涉仪(superconducting quantum interference device, SQUID)并联上一个接地电容C组成。其中SQUID由两个约瑟夫森结并联组成一个环路形成,可以先简单地将其等效成一个约瑟夫森结,等效约瑟夫森能为EJ。根据约瑟夫森关系公式(2)和(3)以及对电容能的计算,量子化后比特的哈密顿量可以写为: 其中EC=e2/2C是电容器中的电荷能量;是库珀对数算符,代表系统中库珀对的数量,是电荷算符;是相位算符,代表系统中库珀对的相位,是磁通算符,Φ0=h/2e是磁通量子。 对于哈密顿量(14),我们依然可以用类似公式(6)的近似方法,将视为一个小量展开cos项。一般为了看出比特能级的非线性,至少需要展开到项,并根据和将哈密顿量二次量子化近似为谐振子的形式,从而得到近似的比特能级分布: 其中是的二阶近似的谐振角频率,即比特的二阶近似本征角频率;n代表系统的第n个能级,n=0代表比特处于|0>态,n=1代表比特处于|1>态,一般比特|1>态与|0>态的频率差就是比特频率。从公式(15)中可以看出,比特每两个能级之间的间隔是不相等的,因此具有非线性,一般比特|2>态和|1>态间的频率差减去比特频率被称为比特的非谐量η。当然,我们还可以继续计算的更高阶近似,从而对比特的能级和哈密顿量进行更精确的修正。 控制线的激发部分是弱耦合微波控制线,需要能够施加高频的微波信号VD,一般信号通过特征阻抗为Z0=50 Ω的传输线后,主要由电容CD耦合到比特上从而激发比特。通过施加频率等于比特|0>态和|1>态频率间隔的微波,可以让比特的状态根据演化,若比特初始处于|0>态,则演化后的状态为: 其中ΩR是拉比角频率,与比特接地电容C、激发耦合电容CD、微波信号幅值VD等相关,刻画了激发信号与比特的相互作用强度。通过控制微波幅值与时间,可以将比特激发到|1>态以及|0>和|1>的任意叠加态。 控制线的偏置原理与1.2节中直接对约瑟夫森结施加直流进行偏置的原理有些不同。首先需要用到由两个约瑟夫森结并联形成环形的SQUID,其等效能量可以表示为: 其中ΦE代表穿过SQUID环的外部磁通。此时,EJ和ϕ都变得与ΦE相关,因此可以通过改变ΦE来改变SQUID的等效能量,从而改变比特能级,起到偏置比特频率的作用。一般在控制线靠近SQUID环的部分有电感LZ,通过对控制线施加直流信号IB,电感产生的磁通就能穿过SQUID环,产生互感MZ,从而可以通过改变直流信号的幅值来改变穿过SQUID环的外部磁通的大小。 读取腔和读取线的部分共同组成了可以通过量子非破坏性(quantum non-demolition, QND)测量读取比特状态的结构。读取腔由一个接地电容CR并联一个接地电感LR组成LC谐振腔,它与比特通过电容CQR产生耦合。读取线是一段特征阻抗为Z0=50 Ω的传输线,可以输入高频微波信号VRin以及接收经过传输线后的信号VRout,在靠近读取腔的部分有电感L,使其与读取腔间能够存在互感MR来产生耦合。 读取腔的本征频率ωR一般高于比特频率ωQ,它们之间的耦合强度为: 由于耦合的存在,导致比特处于不同状态时,读取腔的频率会有微弱的变化,我们将其称为色散位移2χ,在将比特哈密顿量近似到的四阶时,色散位移为: 其中和分别为比特处于|1>态和|0>态时读取腔的角频率,Δ=ωQ-ωR为比特频率和读取腔本征角频率差。 读取腔与读取线的耦合可以用带负载的传输线模型考虑,可以通过读取线进行微波透射频谱S21的测量,探测到读取腔的准确频率,从而区分和,区分比特的状态。这里非破坏性是指我们并没有直接去测量比特的状态,而是通过探测读取腔间接获取比特量子态的信息,最终不改变或几乎不改变比特的初始状态。 为了实现量子态的纠缠,我们可以通过让比特相互耦合来实现。目前最普遍的两比特耦合方式是利用第三个接地Transmon作为可调耦合器来耦合近邻的两个接地Transmon比特[26],可以通过偏置耦合器的频率,改变两比特之间的等效耦合强度。随着比特数的增多,比特的排布也越来越复杂,因此使用浮地Transmon作为比特或耦合器的方案也逐渐成为主流[27,28]。浮地Transmon中约瑟夫森结的两端都是不接地的,这种设计比接地Transmon多了更多的自由度。不过,通过电路或是数学处理后,浮地Transmon在激发、偏置、读取、耦合等方面最终也能得到和接地Transmon类似的结果,我们不在此赘述。 2.2 超导量子计算的实现 本次诺奖工作,构成了超导量子计算从原理验证走向工程实现的关键桥梁。诺奖成果中关键的约瑟夫森结制备与低温测控技术,为此后实用化量子处理器的开发铺平了道路。为了实现图7所示的接地Transmon比特,需要融合芯片制备、低温制冷和微波测控等一系列精密技术,而这些技术的复杂程度正随着人们对更多比特的追求而飞速提升。 目前超导量子计算的实现主要由超导量子比特芯片、稀释制冷机和测控系统组成,如图8所示,芯片封装的样品盒安装在稀释制冷机内部,连接上控制线路后引出到外部的测控系统中。超导量子比特芯片就像电脑CPU中的芯片,是完成计算的核心器件,一般比特和读取腔全部制备在芯片上,而控制线和读取线等布线则部分制备在芯片上,部分由测控系统引入。稀释制冷机用于给芯片提供接近绝对零度的低温环境,并提供芯片与测控系统的连接,一方面保持芯片的超导性,另一方面充分抑制芯片本身产生的以及外部信号引入的噪声。测控系统则是用于给芯片输入各种所需的微波或直流信号,以及接收来自芯片的信号并分析,比如图7中所需发射的激发、偏置、读入、读出信号都是由测控系统发出或接收的。 图8 左图最下方的银色盒子为封装芯片的样品盒;中图为小型稀释制冷机内部结构;右图为部分测控系统 首先我们需要设计出一个芯片,图7所示的单个接地Transmon电路的芯片部分的设计图如图9所示。需要利用版图绘制软件配合微波仿真软件以及2.1小节中介绍的各种原理,将器件结构设计到符合电路所需的参数。电路中所有接地的电极,在芯片上其实就是一整个完整的电极,该电极连接到稀释制冷机的地上从而成为接地电极,而其他所有非地的节点都是独立的多个电极。这些独立的电极可能完全与地断开,因此只存在电容,也可能通过电感或约瑟夫森结等与地相连,它们在芯片设计上都有特定的结构。 图9 单个接地Transmon比特芯片设计图 不过图9所示的设计是单层芯片设计,比特、读取腔、控制线和读取线在同一个芯片上。目前随着比特数的增加,线路的排布成了问题。一方面,比特的控制线和读取线需要被引导至芯片最外圈的引脚,以便连接至外部测控系统;另一方面,比特间通常需要近邻耦合,而耦合的存在使得控制线无法直接穿越相邻比特之间的区域,从而限制了比特在平面芯片上的排列,使其难以突破一维结构。因此,倒装芯片设计成为了一个很好的方案[29]。通过将比特与布线分别制备于两层芯片之上,即便比特呈二维阵列排布,控制线仍可位于另一层芯片上,从而绕过比特之间的物理障碍,并顺利通往阵列中心的比特。这种设计显著提升了比特阵列的可扩展性,使得更大规模的量子计算芯片成为可能。 芯片的制备需要用到大量的微纳加工技术,通过薄膜沉积、光刻、刻蚀、微纳测试和封装等一系列技术完成,常用的工艺需要依次制备作为各个电极的铝,作为压焊过渡层的铌,结构为铝—氧化铝—铝的约瑟夫森结,用于连接线路两边地电极的空气桥,用于压焊的铟柱子,最后进行封装。制备好的空气桥、管状桥和铟柱子如图10(a)所示。不过这套制备工艺并不是唯一方案,不同研究单位由于不同的设备或是技术积累,可能在其中一些步骤或是材料上有所不同,但芯片的基本原理还是一样的。最终,封装好的78比特芯片如图10(b)所示,之后就可以装入稀释制冷机进行测试了。 图10 (a)封装前的布线层电镜图;(b)封装后的78比特芯片照片 稀释制冷机以及测控系统涉及低温工程与微波工程等复杂的学科,目前我们常用的测控系统以及稀释制冷机中的配置如图11所示。制冷机中的不同温度平台起到了逐级降温的作用:50 K盘通过脉管制冷机或GM(Gifford—McMahon)制冷机将氦气从室温冷却到约50 K;3 K盘通过液氦制冷或低温制冷机将氦气冷却到约3K;蒸馏室通过蒸馏过程从氦-3、氦-4混合气体中分离出氦-3用于稀释制冷循环,降温至约800 mK;50 mK盘是保持约50 mK温度的隔离区;混合室通过氦-3、氦-4的混合制冷,实现低于20 mK的极低温环境,用于安装芯片。 图11 测控系统以及稀释制冷机配置示意图 而制冷机中线路上的各种器件也都有着不可或缺的功能:不同温度平台上的衰减器用于逐步衰减噪声、降低信号功率和实现不同温度平台间的直接热传导;红外滤波器用于减少热辐射;低通滤波器进一步抑制高频噪声;隔离器确保读取信号从读入到读出的单向传输,减少反射损耗和串扰;高电子迁移率晶体管(high electron mobility transistor,HEMT)用于放大高频、低噪声的读出信号。 连接制冷机内外的线路主要分为控制线和读取线。控制线包括比特控制线和耦合器控制线,而读取线则分为读入线和读出线。当需要激发比特时,通过任意波形发生器(arbitrary waveform generator,AWG)产生激发脉冲序列,并利用IQ(in-phase and quadrature)混频器将其与微波源(local oscillator,LO)产生的微波信号混合,将脉冲上变频至比特频率以实现比特激发;当需要对比特或耦合器施加偏置时,仅需通过AWG产生直流脉冲序列即可。 读取时,通过混合AWG与LO产生的微波信号,上变频为读入信号输入;再将微波频段的读出信号与LO生成的相同微波信号混合,下变频为读出信号由数模转换器(analog-to-digital converter,ADC)采集。分路器的作用是将LO生成的微波信号均匀分为两路,分别输入到读入线和读出线上的IQ混频器。 通过将封装好的芯片装入稀释制冷机的混合室,并将比特控制线、耦合器控制线以及读取线接入制冷机内部相应的线路中,即可通过外部电子学设备对芯片进行测控表征。一般我们需要先表征单比特的读取耦合、激发与偏置、读取性能以及比特性能等,再表征两比特的比特与耦合器的耦合、比特间的等效耦合以及耦合器性能等,确保比特符合设计的预期。若是芯片可以正常使用,就可以根据芯片的结构和性能,在上面实现量子模拟或量子计算的方案。 2.3 超导量子计算的发展现状与未来 由于建立在宏观量子现象研究的坚实基础之上,以超导量子比特作为量子计算基本单元已经成为目前最有希望实现实用化量子计算的方案之一,近年来,超导量子计算在硬件规模、操控精度和系统集成等方面取得了显著进展。 2014年到2019年间,马蒂尼斯领导谷歌团队攻关超导芯片的多比特集成,并于2018年率先实现了一款9比特芯片[30],而后于2019年实现了53比特“悬铃木”(Sycamore)芯片的量子优越性演示[31]。2024年后,谷歌再次取得重大突破,发布了72比特和105比特的倒装焊超导量子芯片[32—34],为实现更大规模的量子处理器奠定了重要基础。 IBM早在2016年就推出了IBM Quantum Experience量子计算云服务,这是全球首个允许公众通过互联网访问和实验量子处理器的平台,当时提供的是一个5比特的超导量子处理器。2022年,IBM一举将比特数提升至百比特以上,发布了127比特“鹰”(Eagle)处理器[35],2025年又进一步推出156比特“秃鹫”(Condor)处理器。IBM在发展规划上采用“双轨并行”的技术路线, 兼备横向上的高密互联与模块化技术,以及纵向上的硅穿孔与多层布线技术,为未来实现更大规模的量子计算系统奠定了技术基础。 此外,美国加州的量子计算公司Rigetti也已成功研制出84比特芯片;瑞士苏黎世联邦理工学院(ETH)实现了17比特量子处理器的研制[36];美国麻省理工学院成功开发出16比特芯片[37];瑞典查尔姆斯理工大学与芬兰国家技术研究中心(VTT)合作开发出基于硅基铝膜材料的倒装焊量子芯片[38];日本理化学研究所(RIKEN)创新性地采用硅基氮化钛薄膜材料体系,结合硅穿孔三维集成技术,成功研制出高性能量子比特芯片[39];普林斯顿大学长期致力于钽膜电极量子芯片的研究[40,41]。这些成果为中等规模量子处理器的工程化以及超导材料体系的多样化发展做出了重要贡献。俄罗斯国立大学联合量子中心等机构深入探究了铝膜制备工艺对量子比特退相干的影响机制[42],为提升量子比特性能提供了理论基础。而比利时微电子研究中心(IMEC)则开创性地将半导体制造工艺引入量子领域,在12英寸晶圆上实现了超导量子芯片的制备[43],为量子芯片的大规模量产开辟了新路径。 与美国相比,我国的超导量子计算起步较晚,但近几年来也取得了一系列重要进展。2000年左右,中国科学院物理研究所团队基于在超导薄膜和超导机理方面的深厚积累,开始系统性地探索超导器件中的宏观量子隧穿和量子化能级现象。国内首个宏观量子隧穿测量于2006年完成[44],随后在2010—2012年间实现了超导相位比特和磁通比特的关键突破[45]。在2017年成功研制出10比特全联通超导量子处理器,与浙江大学、中国科学技术大学、福州大学等合作实现了多比特纠缠态制备[46,47],之后又开发出更多比特的全联通以及同时带有可调耦合的芯片[48—50]、10比特固定耦合链式芯片[51]、10比特可调耦合链式芯片[52,53]、30比特双链梯子型芯片[54,55]、一维43比特固定耦合芯片“庄子”[56,57],以及二维78比特可调耦合阵列“庄子”2.0[58]。这些成果为量子模拟和多体物理研究提供了重要实验平台。 作为另一个国内最早开展超导量子计算实验研究的团队,南京大学团队于2002年首次实验观测到超导相位量子比特中的量子相干振荡[59],2010年率先演示了3个固态量子比特的量子相干调控[60]。近年来,南京大学团队在探测量子几何张量以及超导量子比特长程耦合新方案上也有突破性进展[61,62]。 近年来,中国科学技术大学在超导量子计算芯片研发领域取得了一系列突破性进展。2021年,团队成功研制出62比特超导量子处理器“祖冲之”号[63];同年,又发布66比特“祖冲之”2.0[64]。在2022年到2023年间,团队持续优化制备工艺,显著提升芯片性能,推出升级版“祖冲之”2.1[65—67]。2024年,研究团队在工艺技术和规模集成方面取得重大突破,成功研制出105比特的“祖冲之”3.0[68]。这一系列研究成果展现了我国在超导量子计算领域的自主研发能力。 浙江大学在超导量子计算芯片研发领域也取得了系列重要突破。2021年,团队成功研制出国际领先的32比特全联通可调腔超导量子芯片[69];2022年,团队在倒装焊技术上取得重大进展,研制出36比特倒装量子处理器[70],并在后续通过设计与制备上的优化显著提升了器件性能[71—74];2024年,浙江大学实现技术跨越,成功研制出121比特“莫干”超导量子芯片[75,76],开展多项前沿量子模拟和纠错方案验证等实验。这些成果为实现实用化量子计算奠定了重要的技术基础。 清华大学团队围绕玻色码的制备、操控和错误探测,发展了一套完整的实验技术体系。2020年,清华大学团队基于二项式纠错码的超导系统首次实现错误透明的相位门操作[77],容错性能显著优于传统方案。2023年,又与深圳国际量子院合作在超导量子线路系统中首次实现了逻辑量子比特的信息存储时间突破盈亏平衡点[78]。 除了高校和传统科研机构外,新型研发机构和科技企业也在超导量子计算领域逐渐发力。2021年北京量子信息科学研究院开发出Flipmon新型量子比特架构[79],并基于该构型成功研制出集成63个Flipmon比特的量子处理器[80];2024年开发出136比特的大规模超导量子芯片,并部署在与中国科学院物理研究所以及清华大学等合作开发的“夸父”量子计算云平台上,为科研用户提供算力服务;2025年成功实现两个独立封装样品盒间量子比特的纠缠[81]。2023年,深圳国际量子院在国际上首次实现了5个独立封装样品盒间量子芯片的互联集成以及纠缠操作[82];2024年在倒装焊技术上再获突破,成功研制出基于钽膜材料的66比特超导量子处理器[83]。中国电信和国盾量子与中国科学技术大学合作开发云平台和电子学测控仪器等上下游软硬件。本源量子发布72比特“悟空”超导量子芯片并探索金融、药物等方面的应用。腾讯量子实验室基于对钽膜超导材料的深入研究[84],成功开发出集成多量子比特的倒装焊芯片[85]。华为技术有限公司通过系统布局,在超导量子芯片领域也进行了许多工作,申请多项专利。量旋科技也开始构建其在超导量子芯片和整机产品方面的业务。 当前,我国超导量子计算已形成多点开花的创新格局,除前述机构外,粤港澳大湾区量子科学中心、湖南师范大学、国防科技大学、福州大学等新型研发机构和高校也已经布局了超导量子计算关键技术和设备的研发,形成了覆盖全国的区域创新网络。 03 总结与展望 2025年诺贝尔物理学奖授予了克拉克、德沃雷特和马蒂尼斯,以表彰他们首次在人造的超导电路中实验证实了宏观量子隧穿与能量量子化这两大现象。他们证明了一个由亿万库珀对组成的宏观系统,其作为一个整体的集体行为也遵循量子力学的规律,这是历史性、奠基性的工作。他们通过精密的低温实验,不仅观测到了代表系统宏观状态的“粒子”量子隧穿出势垒,更利用微波共振激活技术,清晰地揭示了该宏观系统拥有分立的量子化能级。 这一发现远非仅仅是满足了物理学上的好奇心,它成为了超导量子计算发展的基石。获奖工作所揭示的宏观量子效应,为量子比特提供了完美的物理实体,后来科学家们正是利用了该系统最低的两个能级作为信息编码的|0>态和|1>态。更关键的是,约瑟夫森结天然的非线性允许科学家使用特定频率的微波精确地将|0>态激发到|1>态,而不会上升到更高的能级。这项诺奖工作,彻底将一个抽象的量子力学概念,转变成了一个可设计、可制备、可扩展的工程现实。 在此基础上,超导量子计算实现了从原理验证到技术集成的跨越,进入了含噪中等规模量子时代。当前,研究重点已从单纯的量子比特数量竞争,转向构建更长相干时间、更高操控保真度及更低噪声的容错量子系统。展望未来,实现通用量子计算机仍需在比特性能、芯片架构、测控精度及量子纠错等多个工程技术层面取得突破性进展。超导量子计算虽是当前主流技术路线之一,但仍需与中性原子、离子阱及光量子等多种技术路径协同探索与发展。最终目标在于通过量子纠错编码,构建出稳定可靠的逻辑量子比特。面向这一关乎未来的计算革命,采取多元化的技术路径探索战略,持续积累核心技术,方能在机遇来临之际把握主动权。 参考文献 [1] Martinis J M,Devoret M H,Clarke J. Phys. Rev. Lett.,1985,55:1543 [2] Devoret M H,Martinis J M,Clarke J. Phys. Rev. Lett.,1985,55:1908 [3] Gurney R W,Condon E U. Nature,1928,122:439 [4] Gamow G. Zeitschrift für Physik,1928,51:204 [5] de Broglie L V P R. Annals of Physics,1925,2:22 [6] Bardeen J,Cooper L N,Schrieffer J R. Physical Review,1957,108:1175 [7] Anderson M H,Ensher J R,Matthews M R et al. Science,1995,269:5221 [8] Davis K B,Mewes M O,Andrews M R et al. Phys. Rev. Lett.,1995,75:3969 [9] Ivanchenko Y M,Zil'berman L A. Zhurnal Eksperimental'noi i Teoreticheskoi Fiziki,1968,55:2395 [10] Clarke J,Cleland A N,Devoret M H et al. Science,1988,239:992 [11] Kramers H A. Physica,1940,7:4 [12] Fulton T A,Dunkleberger L N. Physical Review B,1974,9:4760 [13] Devoret M H,Martinis J M,Esteve D et al. Phys. Rev. Lett.,1984,53:1260 [14] Hu J,Wu C,Dai X. Phys. Rev. Lett.,2007,99:067004 [15] Ando F,Miyasaka Y,Li T et al. Nature,2020,584:373 [16] Wu H,Wang Y,Xu Y et al. Nature,2022,604:653 [17] Jiang K,Hu J. Nature Physics,2022,18:1145 [18] Zhang Y,Gu Y,Li P et al. Phys. Rev. X,2022,12:041013 [19] Shor P W. Proceedings 35th Annual Symposium on Foundations of Computer Science,1994. pp.124—134 [20] Nakamura Y,Pashkin Y A,Tsai J S. Nature,1999,398:786 [21] You J Q,Nori F. Physics Today,2005,58:42 [22] Wallraff A,Schuster D I,Blais A et al. Nature,2004,431:162 [23] Blais A,Huang R S,Wallraff A et al. Phys. Rev. A,2004,69:062320 [24] Koch J,Yu T M,Gambetta J et al. Phys. Rev. A,2007,76:042319 [25] Barends R,Kelly J,Megrant A et al. Phys. Rev. Lett.,2013,111:080502 [26] Yan F,Krantz P,Sung Y et al. Phys. Rev. Appl.,2018,10:054062 [27] Sete E A,Chen A Q,Manenti R et al. Phys. Rev. Appl.,2021,15:064063 [28] Sete E A,Didier N,Chen A Q et al. Phys. Rev. Appl.,2021,16:024050 [29] Rosenberg D,Weber S J,Conway D et al. IEEE Microwave Magazine,2020,21:72 [30] Neill C,Roushan P,Kechedzhi K et al. Science,2018,360:6385 [31] Arute F,Arya K,Babbush R et al. Nature,2019,574:505 [32] Morvan A,Villalonga B,Mi X et al. Nature,2024,634:328 [33] Acharya R,Abanin D A,Aghababaie-Beni L et al. Nature,2024,638:920 [34] Andersen T I,Astrakhantsev N,Karamlou A H et al. Nature,2025,638:79 [35] Kim Y,Eddins A,Anand S et al. Nature,2023,618:500 [36] Krinner S,Lacroix N,Remm A et al. Nature,2022,605:669 [37] Karamlou A H,Rosen I T,Muschinske S E et al. Nature,2024,629:561 [38] Kosen S,Li H X,Rommel M et al. PRX Quantum,2024,5:030350 [39] Spring P A,Milanovic L,Sunada Y et al. PRX Quantum,2025,6:02034 [40] Place A P M,Rodgers L V H,Mundada P et al. Nat. Commun.,2021,12:1779 [41] Crowley K D,McLellan R A,Dutta A et al. Physical Review X,2023,13:041005 [42] Chudakova T A,Mazhorin G S,Trofimov I V et al. JETP Letters,2024,120:298 [43] Van Damme J,Massar S,Acharya R et al. Nature,2024,634:74 [44] Li S X,Qiu W,Han S Y et al. Phys. Rev. Lett.,2007,99:037002 [45] Yu H F,Zhu X B,Peng Z H et al. Phys. Rev. Lett.,2011,107:067004 [46] Song C,Xu K,Liu W et al. Phys. Rev. Lett.,2017,119:180511 [47] Xu K,Chen J J,Zeng Y et al. Phys. Rev. Lett.,2018,120:050507 [48] Li H K,Li K M,Dong H et al. Chinese Physics B,2019,28:080305 [49] Liu T,Liu S,Li H et al. Nat. Commun.,2023,14:1971 [50] Xu K,Zhang Y R,Sun Z H et al. Phys. Rev. Lett.,2022,128:150501 [51] Chen C T,Shi Y H,Xiang Z et al. Science China Physics,Mechanics & Astronomy,2022,65:110362 [52] Li H,Wang Y Y,Shi Y H et al. npj Quantum Information,2023,9:40 [53] Shi Y H,Yang R Q,Xiang Z et al. Nat. Commun.,2023,14:3263 [54] Xiang Z C,Huang K,Zhang Y R et al. Nat. Commun.,2023,14:5433 [55] Shi Y H,Sun Z H,Wang Y Y et al. Nat. Commun.,2024,15:7573 [56] Shi Y H,Liu Y,Zhang Y R et al. Phys. Rev. Lett.,2023,131:080401 [57] Liu Y,Zhang Y R,Shi Y H et al. Nat. Commun.,2025,16:108 [58] Liu Z H,Liu Y,Liang G H et al. 2025,arXiv:2503.21553 [59] Yu Y,Han S Y,Chu X et al. Science,2022,296:5569 [60] Sun G Z,Wen X D,Mao B et al. Nat. Commun.,2010,1:51 [61] Tan X S,Zhang D W,Liu Q et al. Phys. Rev. Lett.,2018,120:130503 [62] Deng X,Zheng W,Liao X D et al. Phys. Rev. Lett.,2025,134:020801 [63] Gong M,Wang S,Zha C et al. Science,2021,372:948 [64] Wu Y,Bao W S,Cao S et al. Phys. Rev. Lett.,2021,127:180501 [65] Zhao Y,Ye Y,Huang H L et al. Phys. Rev. Lett.,2022,129:030501 [66] Zhu Q,Cao S,Chen F et al. Science Bulletin,2022,67:240 [67] Cao S,Wu B,Chen F et al. Nature,2023,619:738 [68] Gao D,Fan D,Zha C et al. Phys. Rev. Lett.,2025,134:090601 [69] Guo Q,Cheng C,Li H et al. Phys. Rev. Lett.,2021,127:240502 [70] Zhang X,Jiang W,Deng J et al. Nature,2022,607:468 [71] Ren W,Li W,Xu S et al. Nature Computational Science,2022,2:711 [72] Yao Y,Xiang L,Guo Z et al. Nature Physics,2023,19:1459 [73] Zhang P,Dong H,Gao Y et al. Nature Physics,2023,19:120 [74] Xiang L,Chen J,Zhu Z et al. Nat. Commun.,2024,15:4918 [75] Bao Z,Xu S,Song Z et al. Nat. Commun.,2024,15:8823 [76] Xu S,Sun Z Z,Wang K et al. Chin. Phys. Lett.,2023,40:060301 [77] Ma Y,Xu Y,Mu X et al. Nature Physics,2020,16:827 [78] Ni Z C,Li S,Deng X W et al. Nature,2023,616:56 [79] Li X,Zhang Y,Yang C et al. Appl. Phys. Lett.,2021,119:184003 [80] Deng C L,Liu Y,Zhang Y R et al. Phys. Rev. Lett.,2024,133:140402 [81] Song J,Yang S,Liu P et al. Phys. Rev. Lett.,2025,135:050603 [82] Niu J,Zhang L,Liu Y et al. Nature Electronics,2023,6:235 [83] Yang X,Chu J,Guo Z et al. Phys. Rev. Lett.,2024,133:170601 [84] Bu K,Zong Z,Zhang Z et al. Superconductor Science and Technology,2025,38:035010 [85] Bu K,Huai S,Zhang Z et al. npj Quantum Information,2025,11:17